We all share the sorrow and misery from that signal processing class.  You were thrown at some crazy formula, kind of know how to use them but probably never understand why we are doing this after all. I hope this post helps with your lingering confusion to have you realize the power if not the beauty of the tools in your hand.

Consider some vector in a 3D space. It could be represented by rectangular coordinates <x, y, z> or spherical coordinates <r, theta, phi>. It is the same vector, after all, represented using different basis vectors.

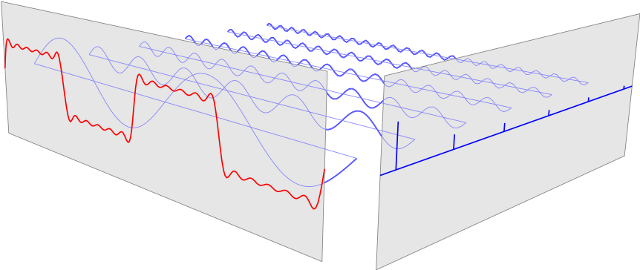
A time-varying signal is no different. It is represented as a linear combination of an infinite set of functions each defined only in only a single point in time and whose time components are separated by an infinitesimal piece. The interesting thing is, we could choose a different set of basis vectors that also span such infinite vector space to represent the very same signal. And this is when the Fourier basis comes into play.

Representing the signal using the Fourier basis essentially transforms the signal from the time domain to frequency domain. Why is this helpful? Well, any two Fourier basis vectors are orthogonal to each other, which means their inner product is zero, which is a fancy way of saying they are “perpendicular” to each other, even though it is hard to visualize what it looks like in the infinite-dimension space. This property makes the calculation of the coefficients of the linear combination of the Fourier basis really easy to derivate.

The full power of Fourier transformation is realized in the LTI system. LTI stands for linear, time-invariant. Any LTI system possesses both scaling and superposition properties. It means if an input signal is represented as a linear combination of Fourier basis vectors, then we could analyze it on a term by term basis, and the final output is the addition of all.

But the punch line is this: each Fourier basis vector is the Eigenfunction of the LTI system, so if it is the input to some LTI, then its output is the same basis vector scaled by an Eigenvalue. The Eigenvalue here is what we referred to as the frequency response of the LTI system, which is also a phasor.

We are using vectors and functions interchangeably in this particular construct. Once we know the frequency response, finding the output signal of this one Fourier basis vector is easy, and the total output is just the sum of outputs from the spectrum of frequencies.