Many inference speedup techniques mirror the classic systems regime—such as caching, paging, tiling, pipelining, and speculative execution (e.g. branch prediction and cache prefetch). Speculative decoding, generalizing speculative execution to stochastic settings, produces several tokens in each forward pass, without changing the output distribution (model quality) or model parameters.

This post discusses two approaches of Speculative Decoding:

1. Speculative sampling with a draft model (2023 paper)
2. Multiple decoding heads with Tree Attention (2024 paper)

Speculative Sampling with a Draft Model

Speculative sampling, or rejection sampling, uses an approximation/draft model—smaller and faster than the model you want to accelerate—to generate $k$ tokens autoregressively and then uses the larger model to verify the $k$ tokens in one pass.

How to verify each speculative token

Let $M_p$ be the target model and $M_q$ be the approximation model.
Let $p(x)$ be the probability of $x$ under $M_p$ (a shorthand for $p(x_t | x_1, \ldots, x_{t-1})$).
Let $q(x)$ be the probability of $x$ under $M_q$.

Sample a token $x$ from $M_q$. Don’t wait for the big model to verify $x$. Continue to sample the next $k$ tokens from $M_q$.

Then, for each speculative token $x$:
If $p(x) \geq q(x)$, accept $x$.
If $p(x) < q(x)$, accept $x$ with probability $p(x) / q(x)$; if $x$ not accepted, sample again from an adjusted distribution of $M_p$, where $p’(x) = norm(max(0, p(x) - q(x)))$.

It is proven that $x$ sampled this way ensures $x \sim p(x)$.

Verify in one pass

The key insight is that the big model can verify the $k$ speculative tokens in one pass. The reason is that in the self-attention mechanism, the big model computes contextualized representations of all prefixes in parallel, i.e. the model outputs

\[p(x_1 | \text{prefix}), \quad p(x_2 | \text{prefix} + x_1), \quad \ldots, \quad p(x_k | \text{prefix} + x_1 + x_2 + \ldots + x_{k-1})\]

simultaneously.

Multiple Decoding Heads with Tree Attention

Choosing the right draft model is hard. What if we just reuse the same model?

Medusa proposes attaching multiple decoding heads to the same model. In the case of 2 heads, head 1 predicts the immediate next token, and head 2 predicts the second token after the prefix. Two heads output at the same time.

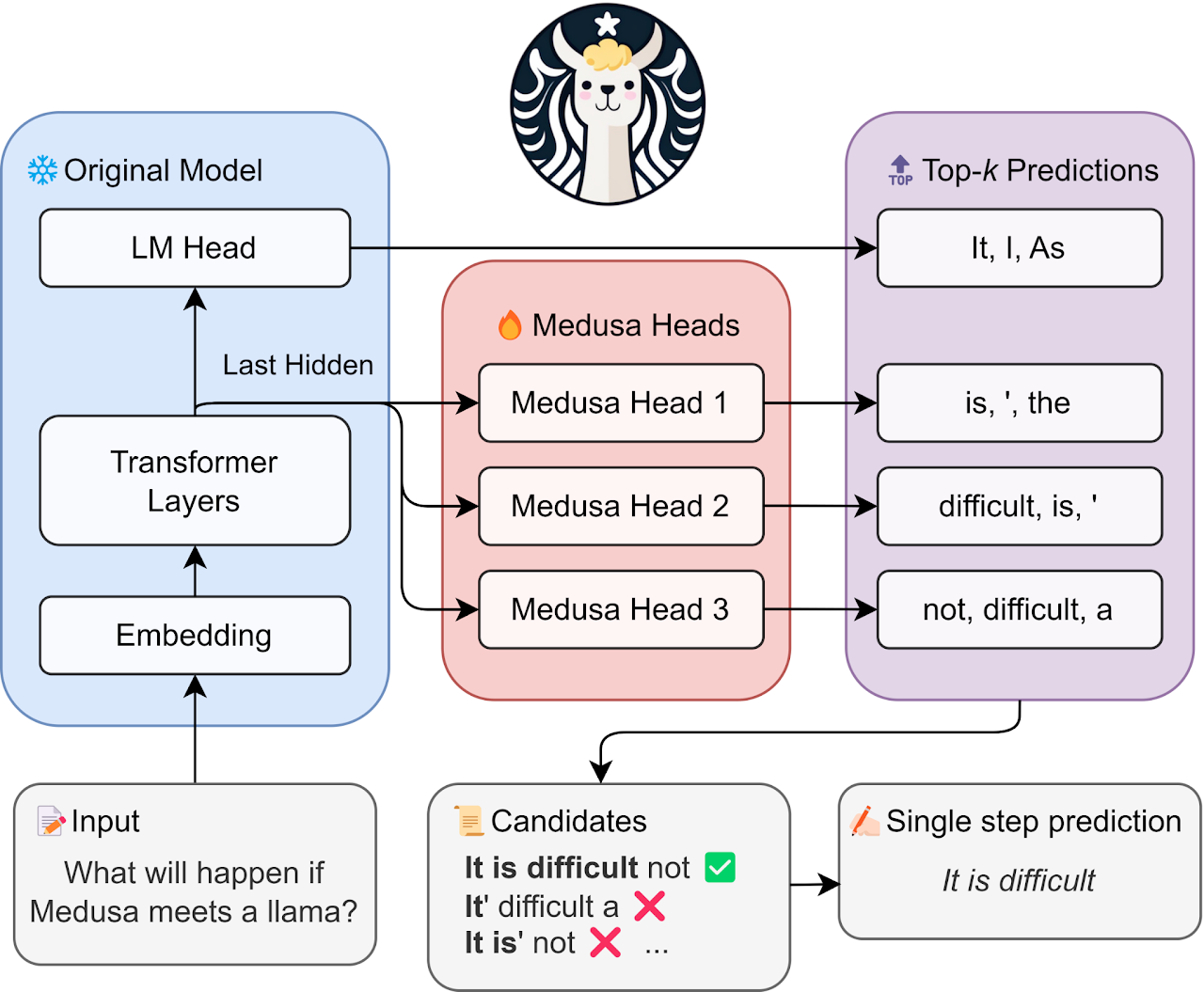
(image source)

Training multiple decoding heads

The standard model only has one decoding head tasked to predict the next token. Thus, to use multiple decoding heads, we need to train the extra heads. The training needs:

• loss function
• tree attention & adjusted positional encoding

Loss function

Use the cross-entropy loss between the prediction of extra heads and the ground truth. To quote the paper:

Given the ground truth token $y_{t+k+1}$ at position $t+k+1$, the loss for the $k$-th head is $L_k = - \log p_t^{(k)} (y_{t+k+1})$, where $p_t^{(k)} (y)$ denotes the probability of token $y$ predicted by the $k$-th head.

We also observe that $L_k$ is larger when $k$ is larger, which is reasonable since the prediction of the $k$-th head is more uncertain when $k$ is larger. Therefore, we can add a weight $\lambda_k$ to $L_k$ to balance the loss of different heads. The final loss is:

\[\mathcal{L}_{\text{MEDUSA-1}} = \sum_{k=1}^{K} -\lambda_k \log p_t^{(k)}(y_{t+k+1}).\]

Tree attention & adjusted positional encoding

Suppose the first decoding head predicts 2 candidates for the next token, and the second decoding head predicts 3 candidates for the next next token. We have a tree of $2 \times 3 = 6$ branches. The tree structure creates two challenges:

1. We need to adjust attention mask such that a token generated from a specific candidate path can only attend to previous tokens within that same path and should ignore other branches.

2. We need to adjust positional encoding because there are multiple candidates for the same position (as in depth in the tree).

The solution is Tree Attention shown below. Note that the attention mask exclusively permits attention flow from the current token back to its antecedent tokens.

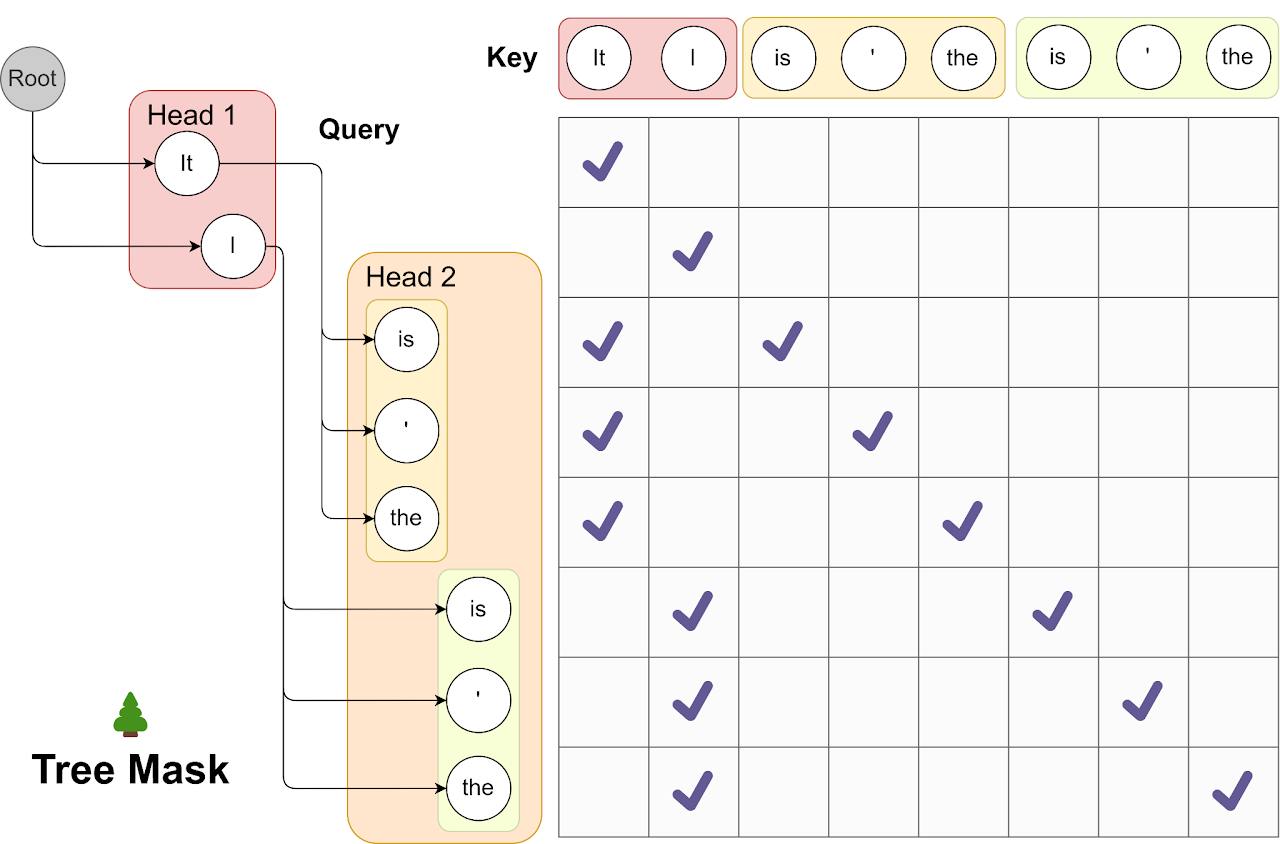
(image source)