5.5x Faster HuggingFace Tokenizers for a Single Sequence

5.5x Faster HuggingFace Tokenizers for a Single Sequence

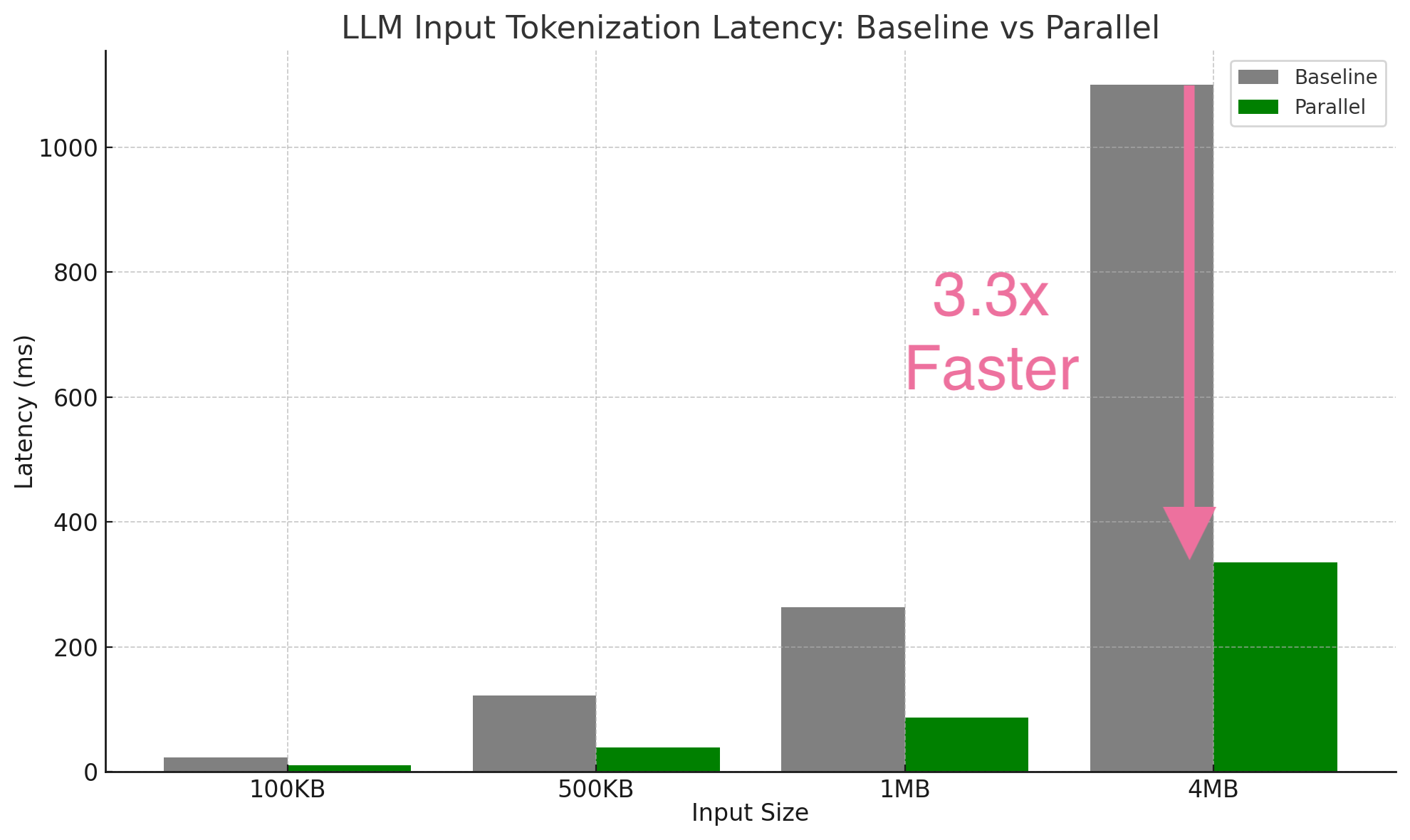
Table of Contents

I made HuggingFace tokenizers encode a single long input on all cores. The Llama 3 tokenizer now encodes 4MB of text 4.9x faster, in 163ms instead of 805ms, and the four tokenizers in the main benchmark are 2.1-5.5x faster at that size. The output is identical to serial encode(): same ids, tokens, offsets and word ids, and not just on the inputs I tried. Each stage of the tokenizer proves that the way the input is cut can’t change its output, and tokenizers that can’t prove it get a slower exact strategy. Fast tokenization is critical to achieve low TTFT given long context.

The Long Context Revolution Has a Bottleneck

LLM models now routinely handle 1M+ token contexts, which enables new use cases:

  • AI Agents: load entire codebases into context instead of fumbling with RAG retrieval.
  • Document Analysis: process entire legal contracts, medical records, or research papers in one shot: no chunking, no context loss.
  • Displacing RAG: Google’s “infinite context” approach suggests a future where retrieval augmentation becomes unnecessary.

But there’s a bottleneck nobody talks about: tokenization. Everyone optimizes inference: quantization, KV cache, flash attention, speculative decoding. But it takes 0.8 seconds to tokenize a 4MB document (935K tokens) with the Llama 3 tokenizer, all on one core. As agents scale with tool use and multi-turn long context, that latency adds straight to TTFT (Time to First Token).

The challenge: a tokenizer reads text left to right. How do you split the work without changing a single token?

Chunking Breaks Tokenization

Split the text in two and encode the halves in parallel, and tokens that span the split come out wrong. The obvious fix is overlapping chunks: encode a margin past the split on both sides, keep each token from the side it starts on. It looks right on prose. It isn’t exact, because what a tokenizer does at a position isn’t decided by a fixed window around it:

Tokenizer Input What overlapping chunks get wrong
GPT-4o a 3000-digit number digits are grouped by 3 from the start of the number; a chunk starting mid-number shifts every group, dropping or duplicating a digit at the seam
GPT-2, Qwen 2.5 3000 = signs BPE merges a whole run in rank order, so a chunk starting mid-run merges it differently
Qwen 2.5, GPT-4o 4000 spaces same, for runs of spaces
BERT a 150-char word serial gives one [UNK] (words over 100 chars); a chunk sees a shorter word and emits ##ac ##gt ...

Where the Time Goes

A HuggingFace tokenizer runs five steps:

  • Normalize. Split out added tokens (special tokens like <|begin_of_text|> or [CLS], matched literally and kept whole), then clean up the text between them: Unicode normalization, lowercasing, stripping accents, replacing spaces with ▁. Every character keeps track of its offset in the original text.
  • Pre-tokenize. Split the normalized text into words (pre-tokens), with a regex (GPT-2, Llama 3) or rules like whitespace and punctuation (BERT). No token ever crosses a word boundary.
  • Model. Turn each word into token ids: BPE applies merges in rank order, WordPiece takes the longest vocabulary match from the left, Unigram picks the most likely split.
  • Build. Collect the ids, token strings, offsets and word ids of all words into one Encoding.
  • Post-process. Truncate to the max length, add the special tokens the model expects ([CLS] … [SEP], a BOS token), and pad.

Here is each step’s share of serial encode() time on 4MB of English prose, for the four tokenizers benchmarked below (Post-process also counts freeing the result, under 1%):

Tokenizer Normalize Pre-tokenize Model Build Post-process
BERT 38% 39% 10% 8% 5%
Llama 3 4% 71% 10% 9% 6%
ALBERT 21% 41% 30% 4% 4%
RoBERTa 4% 61% 24% 8% 3%

The model runs on each pre-token independently, so running it in parallel is exact. But it’s only 10-30% of the time, which caps the speedup at 1.1-1.4x. To go faster, normalization and pre-tokenization must run in parallel too, which means cutting the raw text.

The Idea: Cut Where the Tokenizer Can’t See Across

Cut only at a space between two ASCII letters, like …the lazy|␣dog…. Encode each segment with the full pipeline in parallel, concatenate, post-process once. Almost every tokenizer starts a new word there, and no normalizer combines the space with its neighbors. “Almost” isn’t a proof, so the cut is used only if every stage of the tokenizer proves it safe:

Stage Must guarantee for a + b, cut between them Can’t when
Normalizer normalize(a + b) = normalize(a) + normalize(b), offsets included a regex it can’t analyze
Added tokens no token matches across the cut or grows into it a token ends with a letter, like en_XX
Pre-tokenizer the words of a + b are the words of a, then of b UnicodeScripts, which drops leading spaces
Model deterministic; if a word spans the cut, it’s tokenized as its two halves BPE dropout; WordPiece, Unigram, or BPE without an unknown token on a word spanning the cut

Each stage answers through a new trait method that defaults to “no”, so custom components are never cut. A few cases need care:

  • Start-of-string steps. Prepend("▁") (Llama 2) and Strip act on the start of a string, which a segment isn’t. They get a normalize_continuation that skips those steps.
  • Regex pre-tokenizers. In the GPT-2, cl100k (Llama 3), o200k (GPT-4o), Qwen, DeepSeek, BLOOM and CLIP regexes, a space can only start a match or sit in a whitespace-only match, and nothing looks behind. So a space between two letters always starts a new match, and matching there restarts exactly as at the start of a string. Each of these patterns is allowlisted by its exact text.
  • A word spanning the cut. Llama 2, Mistral and Gemma have no pre-tokenizer: the whole input is one word, and BPE merges 4MB at once. The cut is still exact if no merge can join a symbol ending with a letter to one starting with ▁: each side then merges as if alone, because merges are ordered by rank, then position. A closure over the merge table checks this once per tokenizer.

Of 56 popular tokenizers on the Hub, 54 qualify. The other two have added tokens ending with a letter.

Offsets, Word IDs, and What the Tests Found

Each segment is a slice of the input that keeps its global offsets, so offsets need no shifting, and any step that looks at offsets (like Metaspace prepending ▁ only at offset 0) sees what it sees in serial. Word ids are pre-token indexes, so each segment’s are rebased, minus one when a word spans the cut.

The random tests found one more problem, in serial encoding. Precompiled, the SentencePiece normalizer of T5 and XLM-R, forgets a removed character when it’s the first of a string, like a control character right after a special token. Every later offset in that string then lags by one. Serial carries the lag across the cut; the segment after the cut starts clean, correct but different. Alignments only ever lag, so each cut now checks that the letter before it still maps to its own byte. If it doesn’t, the input is encoded serially.

Then I had adversarial tests written against the proofs, building tokenizers from every component and flag. They found three more gaps, none in a popular tokenizer as shipped:

  • NFC can combine the letter after the space with a following accent (e + U+0301 → é), so the text around the cut is no longer letter, space, ASCII letter, and an added token like y é matches across it. Each cut now checks that shape after normalization, on both sides.
  • BPE without an unknown token drops unknown characters without counting their bytes, so later offsets in the word lag. Cuts inside a word now require an unknown token.
  • Changing the normalizer doesn’t rebuild the added-token matcher. The check now reads the patterns the matcher actually holds.

Fallbacks

  • No safe cut, or no a␣b in the input (Chinese, Japanese): pre-tokenize serially, run the model in parallel.
  • BPE dropout: serial, since serial itself is random.
  • Any error: serial, to return the same error.

The Benchmark Story

Apple M2 Max (8 performance + 4 efficiency cores), 12 threads, Rust release build, no special tokens. Offsets are in bytes, Rust’s default (Python’s are in characters; see below). Inputs are prefixes of Norvig’s big.txt (English prose). The tokenizers are the Hub files google-bert/bert-base-uncased, NousResearch/Meta-Llama-3-8B (a copy of Meta’s), albert/albert-base-v2 and FacebookAI/roberta-base. After warm-up calls, serial and parallel calls alternate, with everyday apps running. Each time includes freeing the returned encoding, and each cell is the median of 62 calls (30 at 4MB) from two separate processes:

Tokenizer 100KB 500KB 1MB 4MB 4MB, serial → parallel (ms)
BERT 3.2x 4.9x 5.1x 5.5x 804 → 147
Llama 3 3.5x 4.7x 4.7x 4.9x 805 → 163
ALBERT 2.0x 2.8x 3.1x 3.2x 1310 → 406
RoBERTa 1.5x 1.9x 2.0x 2.1x 926 → 441

Speedups shift between repeats of the whole benchmark: over three repeats at 4MB, Llama 3 4.7-5.1x, BERT 5.4-5.7x, ALBERT 3.1-3.5x, RoBERTa 2.1-2.2x. Differences smaller than that, between sizes or tokenizers, are noise.

Inputs under 32KB are encoded serially.

Why Llama 3 and BERT stop near 5x. The M2 Max’s 12 cores aren’t equal: 4 of them are slower efficiency cores. And at 4MB:

  • About 40ms of Llama 3’s 163ms, a quarter, runs on one thread: post-processing (about 30ms; TemplateProcessing clones the whole encoding and Encoding::merge copies it again, even with no special tokens to add), freeing the result (about 8ms), and checking the cuts and joining the segments (about 2ms). BERT is similar.
  • Side by side, segments run slower than alone: added up, the 48 segments (4 per thread) take 1.75x (Llama 3) and 1.47x (BERT) as long as the same work does serially.

Not all of it is threads. On one thread, encoding the same 48 segments one after another is already 1.1-1.2x faster than serial for these four. Llama 2 (hf-internal-testing/llama-tokenizer) shows this most. It has no pre-tokenizer, so serial BPE merges all 4MB as one word, which takes 79% of its 1.5 seconds. Cut into the same 48 segments, still on one thread, it takes 779ms (1.9x faster); 12 threads bring it to 147ms, another 5.3x, about 10x in all.

Python’s speedups aren’t comparable with Rust’s. From Python, encode() and encode_parallel() return char offsets, which count characters rather than bytes, as Python strings do. Serial encode() converts byte offsets to char offsets through a hash map with one entry per byte; the parallel path uses a flat array. That makes encode_parallel() 1.3-1.5x faster even on one thread (1.7x for Llama 2, which also gains from cutting), and the same array could make serial encode() faster too. Pulling the other way, the bindings take a shared lock on every model call, which probably slows the parallel path: from Python, Llama 3 and BERT reach 3.9x and 4.0x, below their Rust figures. At 4MB on 12 threads, median of 7 calls each: GPT-2 2.1x, Qwen 2.5 3.2x, GPT-4o 2.4x, T5 3.8x, Gemma 2 7.5x, Llama 2 12.1x.

How I Know It’s Identical

  • A proof per stage: the appendix.
  • Differential tests against serial on 56 Hub tokenizers. Inputs include everything above that breaks overlapping chunks, plus CJK, emoji sequences, combining accents, control characters and special tokens inside text, and seeded random inputs. Each input is cut at every eligible space. Every field of the encoding is compared, for byte, char and no offsets, with and without special tokens, truncation and padding.
  • Adversarial tests that build tokenizers from every normalizer, pre-tokenizer, model and added-token flag, alone and combined, to break the proofs.
  • The same from Python, through encode_parallel.

How to Use It

Rust API

1
2
3
4
5
6
7
8
9

use tokenizers::Tokenizer;

let tokenizer = Tokenizer::from_file("tokenizer.json")?;

// Same result as tokenizer.encode(&text, false)
let encoding = tokenizer.encode_parallel_single(&text, false)?;

// Which strategy this tokenizer gets: Segments, Model or Serial
println!("{:?}", tokenizer.parallel_plan());

Python API

1
2
3
4
5
6
7

from tokenizers import Tokenizer

tokenizer = Tokenizer.from_file("tokenizer.json")
long_text = open("large_document.txt").read()

# Same result as tokenizer.encode(long_text)
encoding = tokenizer.encode_parallel(long_text)

Try It Yourself

The code lives on the parallel branch on github.com/cxuu/tokenizers.

1
2
3
4
5
6
7
8

git clone https://github.com/cxuu/tokenizers.git
cd tokenizers/tokenizers
git checkout parallel
make test  # downloads test data, runs all tests

cargo test --release --test parallel_single_encode
cargo bench --bench parallel_single_benchmark
cargo run --release --example parallel_plans -- data/*.json




Appendix A: Why the Concatenation Is Exact

Let S = A + B, cut at byte c: S[c-1] and S[c+1] are ASCII letters and S[c] is a space. Each step of encoding must give on S what it gives on A, then on B.

Normalization. Each normalizer maps the letter before the cut to a letter and the space to one character (' ', or '▁' after Replace(" ", "▁")), one char at a time around the cut. For Unicode normalization, the space is a starter that never composes with a neighbor. For Precompiled, the space and the letter before it are graphemes of their own, transformed alone. The letter after the space can combine with what follows, so each segment checks after normalization that the cut sits between an ASCII letter and the separator, followed by an ASCII letter, each aligned with its original byte.

Added tokens. Tokens are matched by Aho-Corasick, leftmost-longest, against the patterns the matcher holds. A match crossing the cut would contain the separator with a letter before it; patterns that can are rejected. No token ends with a letter, so none ends at the cut, and rstrip (extend over following spaces) and the single_word check after a match never look across it. A token right after the separator sees it on both sides, so lstrip and single_word agree.

Pre-tokenization. Either some step splits at the cut (BERT and Whitespace remove the space, Metaspace starts a word with ▁, the GPT regexes start a match), after which every step works word by word; or no step does, and the cut stays inside a word.

Model. Inside a word, only BPE qualifies, with an unknown token so that no character is dropped. Let L be the symbols that can end right before the cut: letters, closed under merges (x, l) → m with l in L. Let R be the symbols that can start at it: the separator, closed under merges (r, x) → m with r in R. If no merge pairs an L with an R, no merge ever crosses the cut, and merges on each side happen in the same relative order as when encoded alone.

Offsets and word ids. Segments keep global offsets. A normalizer’s offsets can only lag behind the text, so if the letter before each cut maps to its own byte, nothing lags across it. Word ids are rebased per segment.

Post-processing runs once, on the concatenation, as in serial.